About me

Hi, I'm Adrian! I am a PhD student in the Machine Learning Group at TU Berlin, where my research interests lie in automatic differentiation and explainable AI. I'm a huge fan of the Julia programming language and its community.

I like to spend my free time on open-source software, Go, good coffee and my bike. Some day I'm going to find the time to learn Rust.

Contact

Please reach out if you're interested in collaborating. Links to my Google Scholar and social media profiles can be found at the bottom of this page.

Publications

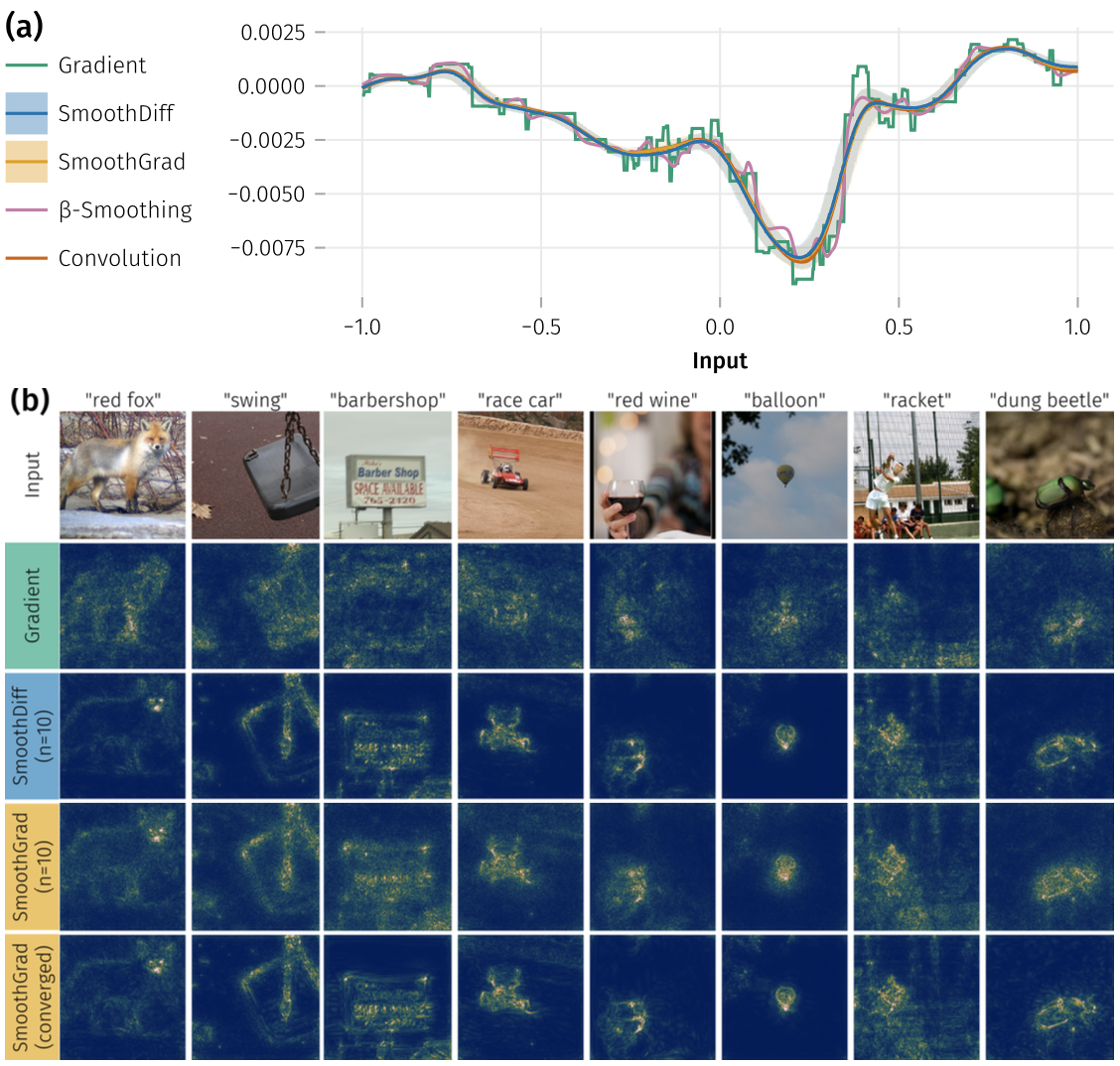
Smoothed Differentiation Efficiently Mitigates Shattered Gradients in Explanations

A. Hill, N. McKee, J. Maeß, S. Bluecher, K.-R. Müller

NeurIPS, 2025

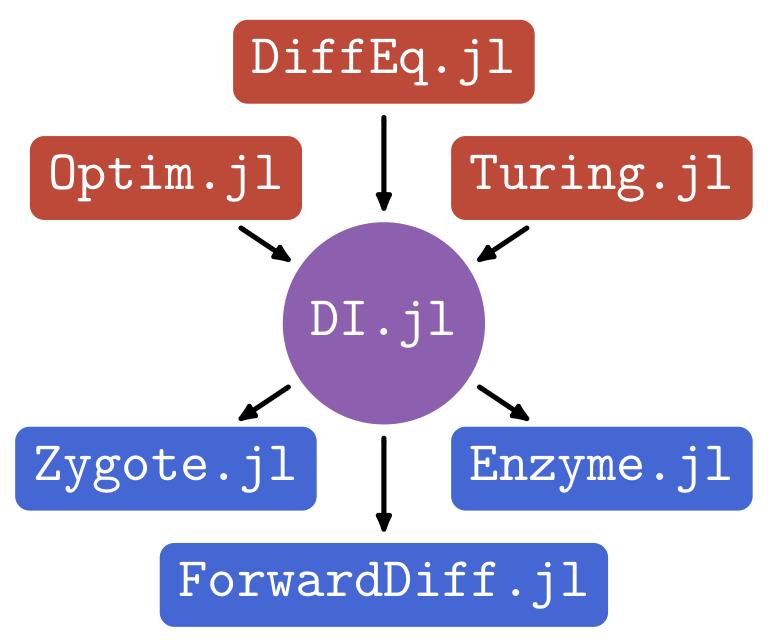
A Common Interface for Automatic Differentiation

G. Dalle, A. Hill

Preprint, 2025

Paper

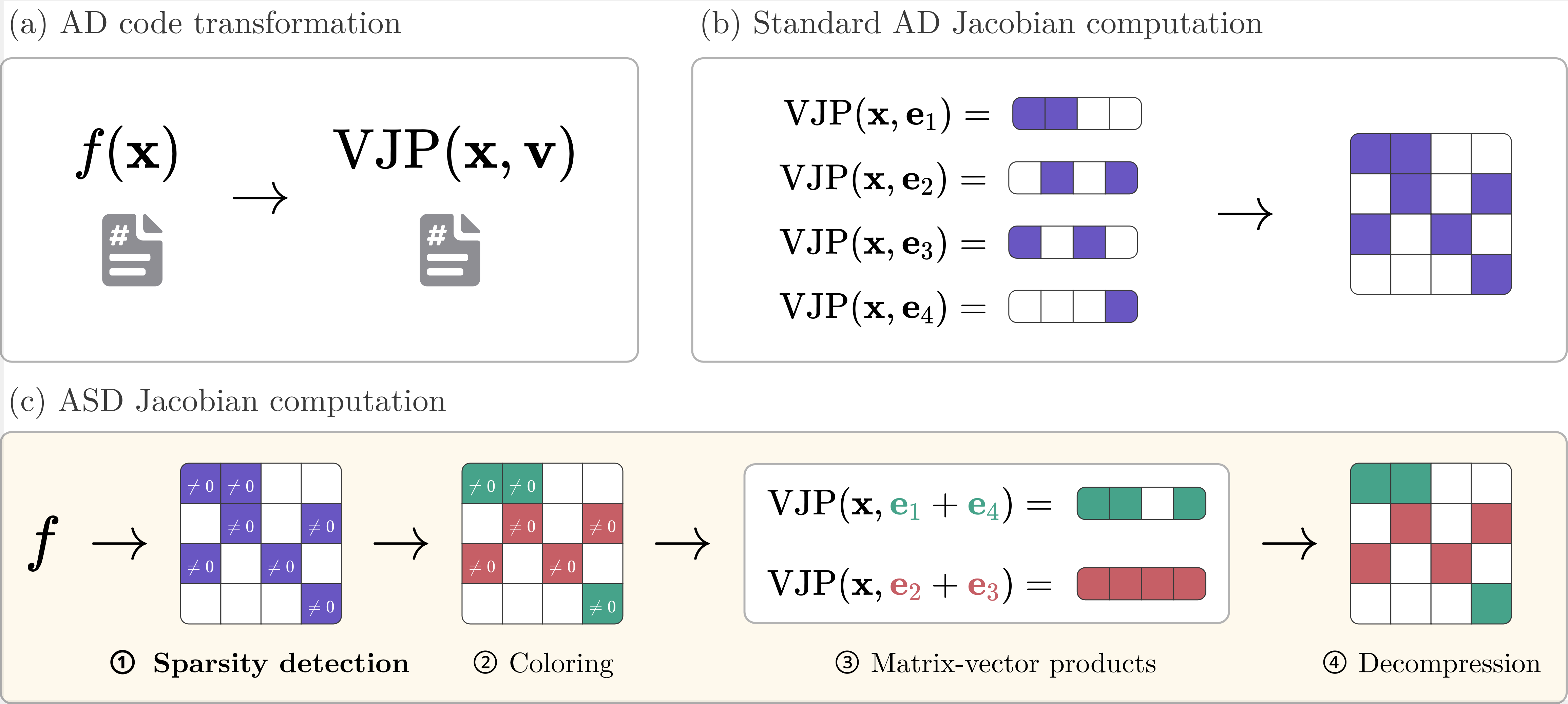
Sparser, Better, Faster, Stronger: Sparsity Detection for Efficient Automatic Differentiation

A. Hill and G. Dalle

TMLR, 2025

Paper

Code

OpenReview

An Illustrated Guide to Automatic Sparse Differentiation

A. Hill, G. Dalle, A. Montoison

ICLR blog post, 2025

Blog

Poster

OpenReview